化學原理啟迪304
Mozart best - Piano Concerto No. 21 C major KV 467 - Andante
1. 氫原子的電子在不同的軌域,能量的大小就會不同。波爾計算出氫原子的電子,在每個軌域運動的能量是:
E=-2.178×10-18J(Z2/n2)
註1:E是圍繞氫原子核公轉的電子的能量。
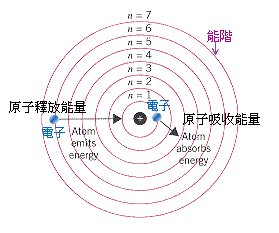
註2:n是電子所處的能階軌域編號,這是一個整數;n的數值愈大,代表電子所處的軌域離原子核愈遠,能階愈高,電子軌域的半徑愈大。
註3:Z是原子量,原子量就是原子的質量,這是依據原子核的質子與中子的數量來決定的。氫的原子核只有一個質子,因此氫的原子量Z=1。
註4:計算出來的能量是「負號-」,因為「原子核的電子」的能量,是以脫離原子核控制的「自由電子」的能量為比較的基準。因為綁在原子核上的電子能量比自由電子低,因此是負數,必須加「負號-」。
註5:「-2.178×10-18J」是圍繞原子核的電子在「最低能階軌域/基態」的能量,這是電子沒有外力干擾下的正常能量,波爾以「電子處於基態的能量」作為衡量「電子在不同能階的能量」的一個標準。
如果電子是處於「最低能階軌域」:n=1,那麼電子的能量就是「-2.178×10-18J」。
2. 脫離原子核的自由電子,不再與原子核交互作用,因此自由電子所處的能階的能量等於0:
E=-2.178×10-18J(Z2/∞)=0
註:∞是無限大,意思是自由電子所處的位置無限遠離原子核。
3. 因為衡量氫原子的電子的能量標準是「自由電子的能量=0」,因此圍繞氫原子的電子不論在任何軌域,能量都是負的。
4. 當氫原子的電子受到外力介入而改變軌域/能階時,能量改變的幅度是多少?我們可用方程式「E=-2.178×10-18J(Z2/n2)」分別計算電子在不同能階的能量,然後相減,就得到改變的能量。
5. 舉例來說,假設有一顆氫原子從激態回復到最低能階-基態ground,它的電子從激態能階n=6掉落到基態能階n=1。
6. 我們用方程式計算電子的能階,因為氫原子核只有1個質子,所以Z=1,處於激態n=6與基態n=1的電子的能量是:
For n=6: E6=-2.178×10-18J(12/62)=-6.05×10-20 J
For n=1: E1=-2.178×10-18J(12/12)=-2.178×10-18J
7. 特別留意,基態電子的能階n=1的負能量,大於激態電子的能階n=6,這代表電子在最小的電子軌域時,受原子核控制的力量比較大。
8. 當電子從激態能階n=6,落到基態能階n=1,能量變化是
ΔE
=最終狀態的能量-最初狀態的能量
=E1-E6
=(-2.178×10-18J)-(-6.05×10-20J)
=-2.118×10-18J
能量的改變的符號是「負號-」代表原子失去能量,進入比較穩定的狀態;從高能階軌域n=6轉換到低能階軌域n=1的過程中,電子多餘的能量轉化成光子,釋放出去。
沒有留言:
張貼留言