化學原理啟迪320
1. Steven S. Zumdahl:盒中粒子模型有二面牆,粒子從第一面牆到第二面牆的波動函數也必須是0,我們可以寫成ψ(L)=A sin(kL) =0;其中,k是nπ/L的數值,n是整數(1、2、3……)。意思是,
ψ(x)=A sin〔(nπ/L)‧x〕
2. 因此
ψ(L)=A sin〔(nπ/L) ‧L〕=A sin(nπ) =0
Bach - Suite no. 1 in G for cello - Mischa Maisky
3. 徐弘毅:盒中粒子模型,模擬電子圍繞原子核公轉的模型,粒子代表電子,粒子沿著橫向的x軸移動,L是盒子的寬度,也是粒子單次移動的最長距離,粒子沿著x軸來回移動一次的距離是2L,代表電子圍繞原子核公轉一圈。
4. 我們知道,圍繞原子核的電子並不是筆直前進的,而是在旋轉中前進,那麼當電子在軌道上前進一段距離時,它到底自轉多少度?需要一個換算的比例,這個換算的比例就是k。
5. 盒中粒子在x軸上移動的一段距離乘上k(nπ/L),就等於電子自轉的角度或弧度。
6. Steven S. Zumdahl:為了弄清楚常數A的數值,我們必須引進一個新的觀念。應用波動力學去描述物質,科學家已經知道「波動函數的平方」與「粒子存在於空間中某一個點的機率」之間的關係。
7. 這代表波函數的平方能計算出,在某個特定的位置點附近找到那一顆粒子的機率。這個概念與盒中粒子的模型設定邊界條件有關,因為盒中粒子在每一個點的機率總和應該是1。
8. 更精確地說,在x軸上的其中一段長度dx的x位置點附近,發現這顆粒子的機率是ψ2(x)dx。
9. 徐弘毅:為什麼波動函數的平方與「粒子存在於空間中某一個點的機率」之間有關?
10. 電子圍繞軸心旋轉到某個角度的位置時,我們從這顆電子的位置畫一條垂直線到平衡線的位置,這是電子旋轉角度的對邊;再從電子連接到圓心的畫一條直線,這條直線是直角三角形的斜邊,也是電子旋轉軌跡的半徑,再加上平衡位置線為底,這樣就做出一個直角三角形。
11. 函數sine就是直角三角形的對邊÷斜邊=「這顆電子與平衡位置的距離÷這顆電子旋轉軌跡半徑」的比例。
12. 函數sine的平方是計算「這顆電子與平衡位置的距離平方÷這顆電子旋轉軌跡半徑的平方」。這是計算「對邊構成的正方形面積」占「斜邊面積的比例」。
13. 基本上波函數Asin kx,也就是旋轉角度kx的sin函數,還要再乘上振幅A,振幅也是電子旋轉軌跡的半徑。所以波函數平方是:
「電子旋轉軌跡的半徑的平方」×「這顆電子與平衡位置的距離平方÷這顆電子旋轉軌跡半徑的平方」=這顆電子與平衡位置的距離平方
14. 我們可以想像,當電子非常靠近平衡位置時,它的波函數平方會比較接近零,數值較小,如果電子非常靠近波峰或波谷的位置,它的波函數平方會比較大,這代表什麼意思?
15. 量子力學家薛丁格應該是認為,能量粒子並不是等速上下波動的。能量粒子通過平衡位置附近的時候速度較快,波峰或波谷附近的位置速度較慢;所以代表電子位置的波函數平方顯示,電子出現在平衡位置附近區域的機率較小,出現在波峰或波谷附近的機率較高。
16. 能量粒子的波狀運動並非等速有沒有道理呢?如果用單擺來看有點道理,單擺從最高點落下到最低點過程是不斷加速的,從最低點再擺到另一端的最高點是不斷減速的,所以,以時間來看,單擺出現在兩端最高點的時間比率會比較高一點,也就是機率較高。
17. 不過薛丁格凍結超高速的電子波動,用慢動作來分析電子位置的作法,是受到海森堡質疑的,海森堡認為當我們對一個高速運動的量子(例如圍繞原子核的電子)進行測量時,如果能夠準確地測量出它的位置,那麼計算出來的能量就會失真很多。
18. 盒中粒子是模擬原子的電子軌域,如同電子軌域有其固定大小,盒子是一個有限的空間,粒子只能沿著x軸來回移動,不會跑到其他地方,所以,電子出現在x軸上每一點的機率合起來應該是1。
19. 再複習一次,當我們觀察圍繞原子核的電子時,我們是在軌道上切下一個剖面,從剖面觀察電子圍繞軌域中心軸旋轉的情形,不考慮電子在旋轉的同時還會「往前推進一段距離」這個問題。
20. 當我們考慮到電子出現在三度空間的某一個位置的機率時,就必須要考慮到電子波動時是會往前進的,因此粒子在波動出現的機率ψ2(x)必須再乘上前進的距離dx,才是電子出現在某一段波動區域的真正機率。
21. Steven S. Zumdahl:因為盒中只有1顆粒子,所以粒子沿著x軸移動(從x=0到x=L)的機率總和必須是1。我們把盒子總長(從x=0到x=L)所有粒子出現的機率加起來是:
發現盒中粒子的總機率=∫L 0ψ2(x)dx=1
注:粒子在盒子裡面移動過程是以波的形式前進的,波動到每一個位置點的機率,用微積分∫L 0累加起來,總機率是1。
22. 代入ψ(x)=Asin[(nπ/L)‧x],我們得到
∫L 0ψ2(x)dx=∫L 0A2sin2[(nπ/L)‧x] dx=1
或∫L 0sin2[(nπ/L)‧x] dx=1/A2
23. 中間數是L/2,這代表
L/2=1/A2 並且 A=√2/L
24. 徐弘毅:A是波的振幅,也就是波的最高點或最低點到平衡位置的距離。首先,不要忘記圍繞原子核的電子在空間中是旋轉中前進的,並不是扁平的波,第二、量子運動速度很快,瞬間就遍佈每一個位置,所以不能光直線的觀點來衡量量子,應該用平面去攔截瞬間遍佈圓平面的量子。
25. A2是用一個平面攔截波,計算一個振幅的能量攤平在平面上的面積大小,面積上的每一個能量單位反映出波狀運動的量子(圍繞原子核的電子)在單一個振幅中的每一個能量單位。
26. 一個振幅上只有一顆量子(電子),所以一個振幅範圍內出現1顆量子的總機率是1,振幅上每一個能量單位出現的量子的機率是1/A2。
27. 如果振幅A數值小於1,量子出現的機率1/A2有可能大於1,這代表波的振動速度很快,因此同一個振幅區間同時出現無數顆量子。
28. 一般人對量子最難以想像的部分是量子的移動速度太快,快到同一個時間內,量子在同一個空間中出現無數顆分身,超快的移動速度使得一顆量子變成數億顆量子。
29. 盒中粒子模型是模擬圍繞原子核公轉的電子,請問盒中粒子移動過程中,出現在振幅範圍內的機率有多少?
30. 我們知道,電子波狀運動的時候,有一半的機率會出現在正的振幅區域,也就是波峰到平衡位置的區域,另一半機率出現在負的振幅區域,也就是平衡位置到波谷的區域,所以粒子前進過程中,有一半的機率會出現在正的振幅區域內L/2。
31. 所以盒中粒子在振幅範圍內出現的機率L/2就是波動的電子在振幅範圍出現的機率1/A2。由此推算出振幅A=√L/2
32. Steven S. Zumdahl:現在我們知道k和A的數值,那麼我們就可以知道在一度空間的盒中粒子的波動函數
33. 我們也可以把k的數值代入能量方程式
E=ℏ2k2/2m=[2 ℏ2(nπ/L) 2]/2m
34. 將ℏ=h/2π得到
35. 特別留意,當我們把各種整數代入薛丁格方程式,會得到一系列的答案,使每一種位置的粒子的波動函數都反應它們特定的能量狀態
n 翻譯編寫Steven S. Zumdahl 《Chemical Principles》
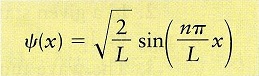


沒有留言:
張貼留言