化學原理啟迪319
1. Steven S. Zumdahl:把運算子輸入薛丁格方程式ĤΨ=EΨ,得到
-ℏ2/2m‧d2Ψ/dx2=EΨ
注:Ψ是波函數。
我們重新排列這個方程式得到
(d2/dx2)Ψ=-(2mE/ℏ2)Ψ
Brendel plays Schubert Impromptu Op.90 No.3
2. 我們的目標是找到符合這個方程式的特定波函數Ψ(x),特別留意這個方程式的解答d2Ψ/dx2=(常數constant)Ψ函數,這就是依據薛丁格方程式解出的波函數,它的第二個衍生數一定跟原始波函數的形式一樣。一個波函數如果符合這個原則,它就是sine函數(正弦)。
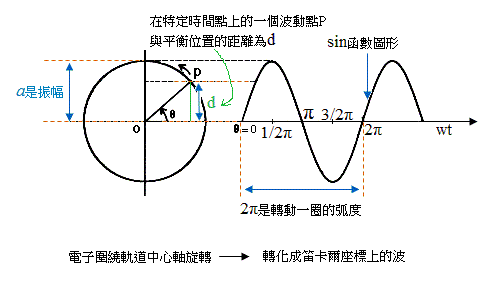
3. 徐弘毅:波函數Ψ用來描述原子在特定能階上的電子的波狀運動,圍繞原子核的電子的波狀運動是有規律的,每個特定能階上的電子都有固定的波長、週期、振福。
4. 電子在第一個波的某一個位置點(第一個衍生數),轉過一個(或數個)週期之後會再回到同一個位置點(第二個衍生數),這就是所謂的「第二個衍生數一定跟原始的波函數一樣」。波的週期,就是一個完整的波長,或是自轉一圈的角度360°或弧度2π。
5. sine函數是以x軸的0為起點往上形成一個高峰,然後再下降穿過x軸形成一個凹谷,再往上穿過x軸形成一個高峰……,如此週而復始的波。在這裡x軸上的數字指的是,在不同時間點粒子旋轉的角度或弧度。
6. 這個波形來自於圍繞著中心軸一圈又一圈反覆旋轉的電子,我們把電子轉到每一個角度時,它與穿過中心軸的橫軸之間的距離用d代表,一一記錄在笛卡爾座標上,就出現一個以0為起點週而復始的波形,也就是一個sine函數。
7. 圍繞著中心軸旋轉的電子,也可以拿穿過中心軸的縱軸為標準,測量電子在各個角度與縱軸之間的距離d,一一記錄在笛卡爾座標上,就出現一個以波峰最高點為起點週而復始的波形,這樣的圖形是一個cosine函數圖形。在薛丁格推論第二衍生數的過程中,為了抓出公式的重點,他把sine函數改為cosine函數。
8. Steven S. Zumdahl:舉例來說,假設函數A sin(kx),A和k是常數,現在我們要找到這個函數沿著x軸產生的第二個衍生數。
(d2/dx2)(A sin kx)
=(A d/dx)(d sin kx/dx)=(A d/dx)(k cos kx)
=Ak(d cos kx/dx)= Ak(-k sin kx)
=-Ak2 sin kx=-k2(A sin kx)
9. 徐弘毅:依據簡單諧和運動的定義the Definition of Simple Harmonic Motion,一個有週期性的波,在特定時間點上的一個波動點與平衡位置的距離設定為d。
d=a sin wt 或d=a cos wt
l a是振幅,這是從最高點到平衡位置,或從最低點到平衡位置的距離。
l 2π/w是週期,2π是轉動一圈的弧度(360°),w是每秒波動的總共弧度(或角度),轉動一圈的距離除每秒波動的距離2π/w得到粒子轉動一圈的時間-週期。
l w/2π是頻率,w是每秒波動的距離(總共轉了多少弧度),2π是轉動一圈的距離(轉一圈的弧度),每秒波動的距離除轉動一圈的距離w/2π,得粒子每秒的轉動的次數-頻率。
10. 薛丁格方程式中的A sin kx與簡單諧和運動的公式定義看起來一樣,A就是指振幅a,wt就是kx,這是粒子在某一個時間點的角度,其中k推測是調整粒子回到下一個週期的比例數值。
11. (d2/dx2)(A sin kx)=-k2(A sin kx):薛丁格推算後發現,粒子從第一個週期的某一個點,再轉一圈回到第二個週期的同一點,都要乘上某個常數,左邊波函數A sin kx乘上d2/dx2,右邊波函數A sin kx乘上-k2。
12. Steven S. Zumdahl:結果我們發現
[d2(A sin kx)]/dx2=-k2 (A sin kx)
這個波狀函數方程式與盒中粒子模型推論出來的薛丁格方程式,模式相同。
透過盒中粒子推論出的薛丁格方程式:
( d2 /dx)2Ψ=-(2 m E/ ℏ2)Ψ
注:Ψ是波函數,就是A sin kx。
與這個方程式比較
(d2/dx2)(A sin kx)=-k2 (A sin kx)
以上二個方程式等號左邊是相同的( d2 /dx)2Ψ就是(d2/dx2)(A sin kx),因此右邊波函數的係數也是相同的
-k2=- 2mE/ ℏ2
重新排列得到能量的方程式
E=ℏ2 k2/2m
徐弘毅注:E=ℏ2 k2/2m 是原子的某一顆電子的能量方程式。
沒有留言:
張貼留言